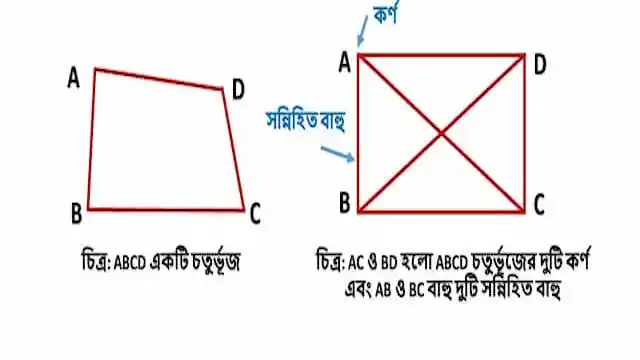
চতুর্ভুজ কাকে বলে চতুর্ভুজ এর বৈশিষ্ট্য ও প্রকারভেদ

চারটি রেখাংশ দ্বারা আবদ্ধ ক্ষেত্র একটি চতুর্ভুজ। অর্থাৎ কোনাে সমতলে চারটি সরলরেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে চতুর্ভুজ বলা হয়। একটি চতুর্ভুজের চারটি বাহু, চারটি কোণ, চারটি শীর্ষবিন্দু এবং দুইটি কর্ণ থাকে। চিত্রে AB, BC, CD ও DA রেখাংশ চারটি সংযােগে ABCD চতুর্ভুজ গঠিত হয়েছে।

A, B, C ও D চারটি কৌণিক বিন্দু বা শীর্ষবিন্দু। ABC, BCD, CDA ও DAB কোণ চতুর্ভুজের চারটি কোণ। A ও B শীর্ষবিন্দু যথাক্রমে C ও D শীর্ষের বিপরীত শীর্ষবিন্দু। AB ও CD বাহু পরস্পর বিপরীত বাহু এবং AD ও BC বাহু পরস্পর বিপরীত বাহু।

• চতুর্ভুজের চারটি বাহু থাকে
• চতুর্ভুজের চারটি কোণ থাকে
• চতুর্ভুজের চারটি কোণের যােগফল = ৩৬০°
• চতুর্ভুজের দুটি কর্ণ থাকে
• চতুর্ভুজ একটি বহুভূজ
• চতুর্ভুজের চারটি শীর্ষবিন্দু ও চারটি শির:কোণ থাকে
• চতুর্ভুজের চারটি বাহুর সমষ্টিকে পরিসীমা বলে

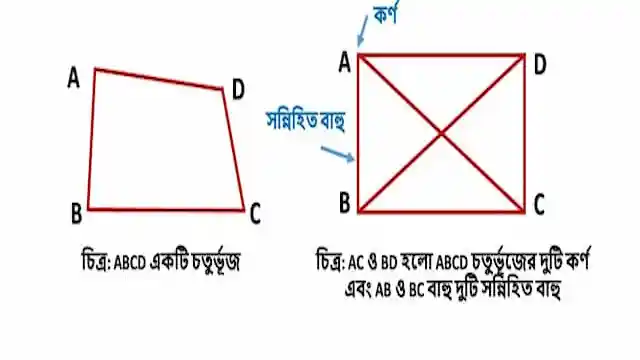
চতুর্ভুজের সন্নিহিত বাহু : একটি শীর্ষবিন্দুতে যে দুইটি বাহু মিলিত হয় এরা সন্নিহিত বাহু। যেমন : চিত্রে AB ও BC বাহু দুইটি সন্নিহিত বাহু।

চতুর্ভুজের কর্ণ : চতুর্ভুজের বিপরীত বিন্দুদ্বয়ের সংযােজ রেখাংশকে কর্ণ বলা হয়। চিত্রে AC ও BD হলাে ABCD চতুর্ভুজের দুইটি কর্ণ।

চতুর্ভুজের পরিসীমা : চতুর্ভুজের চারটি বাহুর দৈর্ঘ্যের সমষ্টিকে এর পরিসীমা বলা হয়। ABCD চতুর্ভুজের পরিসীমা (AB + BC+CD + DA) এর দৈর্ঘ্যের সমান।

১. সামান্তরিক : যে চতুর্ভুজের বিপরীত বাহুগুলাে পরস্পর সমান্তরাল তা সামান্তরিক। সামান্তরিকের সীমাবদ্ধ ক্ষেত্রকে সামান্তরিক ক্ষেত্র বলে।

• সামান্তরিকের বিপরীত বাহুগুলাে পরস্পর সমান ও সমান্তরাল।
• সামান্তরিকের বিপরীত কোণগুলাে সমান।
• সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।

বিশেষ দ্রষ্টব্য : রম্বস, আয়ত ও বর্গ প্রত্যেকেই এক একটি সামান্তরিক। লক্ষ করি, সামান্তরিকের সংজ্ঞানুসারে শুধু বিপরীত বাহুগুলাে সমান্তরাল হলেই সামান্তরিক এখানে কোণের ব্যাপারটি আগ্রাহ্য। প্রত্যেকেরই বিপরীত বাহুগুলাে সমান্তরাল, তাই প্রত্যেকেই এক একটি সামান্তরিক।

২. আয়ত : যে সামান্তরিকের একটি কোণ সমকোণ, তাই আয়ত। আয়তক্ষেত্র এমন একটি সামান্তরিক যার প্রত্যেকটি কোণ এক সমকোণ।

• যে সামান্তরিকের একটি কোণ সমকোণ, তাই আয়তক্ষেত্র।
• আয়তের প্রত্যেকটি কোণ সমকোণ এবং বিপরীত বাহুগুলাে সমান।
• আয়তের কর্ণদ্বয় সমান এবং এরা পরস্পরকে সমদ্বিখণ্ডিত করে।

৩. রম্বস:  রম্বস এমন একটি সামান্তরিক যার প্রতিটি বাহুর দৈর্ঘ্য সমান।

• যে সামান্তরিকের দুইটি সন্নিহিত বাহু সমান, তাই রম্বস।
• রম্বসের বাহুগুলাে সব সমান এবং বিপরীত কোণগুলাে সমান।
• রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।

৪. বর্গ : বর্গ এমন একটি সামান্তরিক যার প্রত্যেকটি কোণ সমকোণ এবং বাহুগুলাে সমান। আবার, বর্গ এমন একটি আয়ত যার সন্নিহিত বাহুগুলাে সমান।

• যে আয়তের দুইটি সন্নিহিত বাহু সমান তাই বর্গ।
• যে সামান্তরিকের দুইটি সন্নিহিত বাহু সমান এবং একটি কোণ সমকোণ তাই বর্গ ।
• বর্গের বাহুগুলাে সমান এবং প্রত্যেকটি কোণ সমকোণ।
• বর্গের কর্ণদ্বয় সমান এবং পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।

৫. ট্রাপিজিয়াম : যে চতুর্ভুজের এক জোড়া বিপরীত বাহু সমান্তরাল, একে ট্রাপিজিয়াম বলা হয়। ট্রাপিজিয়ামের সীমাবদ্ধ ক্ষেত্রকে ট্রাপিজিয়ামক্ষেত্র বলে। চিত্রে ABCD একটি ট্রাপিজিয়াম

৬. ঘুড়ি : যে চতুর্ভুজের দুই জোড়া সন্নিহিত বাহু সমান, একে ঘুড়ি বলে।

লক্ষণীয়: সামান্তরিক, রম্বস, আয়ত ও বর্গ প্রত্যেকের ক্ষেত্রেই বিপরীত বাহুগুলাে সমান ও সমান্তরাল।

• সকল রম্বস সামান্তরিক কিন্তু সকল সামান্তরিক রম্বস নয়।
• সকল আয়ত সামান্তরিক কিন্তু সকল সামান্তরিক আয়ত নয়।
• সকল বৰ্গই সামান্তরিক কিন্তু সকল সামান্তরিক বর্গ নয়।
• সকল বৰ্গই রম্বস কিন্তু সকল রম্বসই বর্গ নয়।
• সকল বৰ্গই আয়ত কিন্তু সকল আয়ত বর্গ নয়।
• চতুর্ভুজের চারটি কোণের সমষ্টি চার সমকোণ। A + B + C + D =360 ডিগ্রি।
• চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করলে তা একটি সামান্তরিক।
• সামান্তরিকের কর্ণদ্বয় পরস্পর সমান হলে তা একটি আয়ত।
• আয়তের সন্নিহিত বাহুর মধ্যবিন্দুসমূহের যােগে যে চতুর্ভুজ হয় তা একটি রম্বস।