ত্বরণ কাকে বলে? মন্দন কাকে বলে? ত্বরণ এর একক, মাত্রা ও সূত্রাবলি।

যখন কোনো বস্তু সমবেগে যায় তখন তার কোনো ত্বরণ নেই। বেগের পরিবর্তন হলেই বুঝতে হবে সেখানে ত্বরণ রয়েছে। আরো সুস্পষ্ট করে বললে বলতে হবে ত্বরণ হচ্ছে সময়ের সাথে বেগের পরিবর্তনের হার। বেগের যেহেতু দিক এবং মান দুটিই আছে তাই বেগের পরিবর্তন দুভাবেই হতে পারে।

ত্বরণ কাকে বলে?

ত্বরণ এর সংজ্ঞাঃ

সময়ের সাথে পারিপার্শ্বিকের সাপেক্ষে কোনো বস্তুর বেগ বৃদ্ধির হারকে ত্বরণ বলে।

মন্দন এর সংজ্ঞাঃ

সময়ের সাথে পারিপার্শ্বিকের সাপেক্ষে কোনো বস্তুর বেগ হ্রাসের হারকে মন্দন বলে।

ত্বরণ কি?

মনে কর তুমি যখন আঁকাবাঁকা পথে সাইকেল চালিয়ে যাচ্ছ, তখন যতবার তুমি বাঁক নিয়েছ ততবার তোমার বেগের পরিবর্তন হয়েছে অর্থাৎ তোমার ত্বরণ হয়েছে। তুমি পুরো পথটুকু সমদ্ৰুতিতে গিয়ে থাকলেও শুধু দিক পরিবর্তনের জন্য ত্বরণ হয়েছে। তুমি যদি একটা পাথরকে সুতা দিয়ে বেঁধে মাথার উপর সমদ্রুতিতে ঘোরাতে থাক তাহলে ঘুরতে থাকা পাথরটির ক্রমাগত দিক পরিবর্তন হবে। অর্থাৎ তার বেগের পরিবর্তন হবে বা ত্বরণ হবে। যদি তোমার গতি সরলরৈখিক হয়ে থাকে তাহলে দিক পরিবর্তনের কোনো সুযোগ নেই। তার ত্বরণ হতে পারে শুধু বেগের মানের (দ্রুতির) পরিবর্তনের কারণে। (যদি বেগের মান বাড়তে থাকে তাহলে আমরা বলি বেগের দিকে বস্তুটির ত্বরণ হচ্ছে। যদি বেগের মান কমতে থাকে আমরা বলি বস্তুটির ঋণাত্মক ত্বরণ বা মন্দন হচ্ছে। আমরা এখন সরলরেখায় চলমান কোনো একটি বস্তুর ত্বরণ বের করতে পারি। উদাহরণ হিসেবে আমরা নিচের লেখচিত্রটি দেখতে পারি-

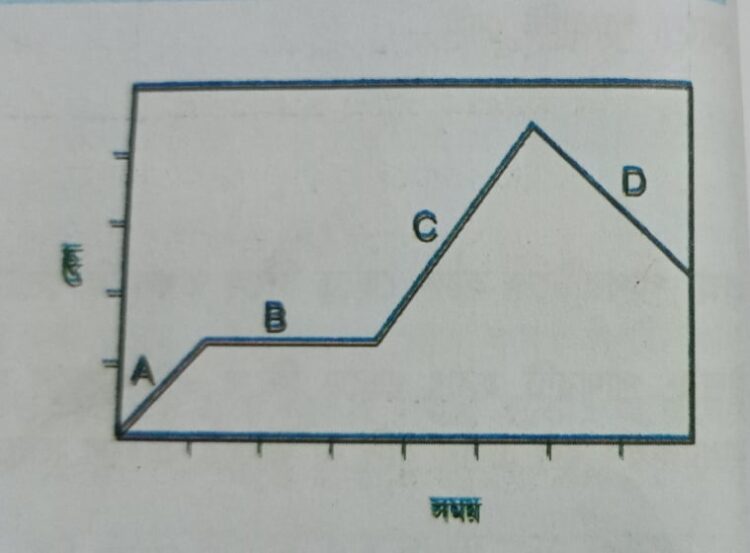
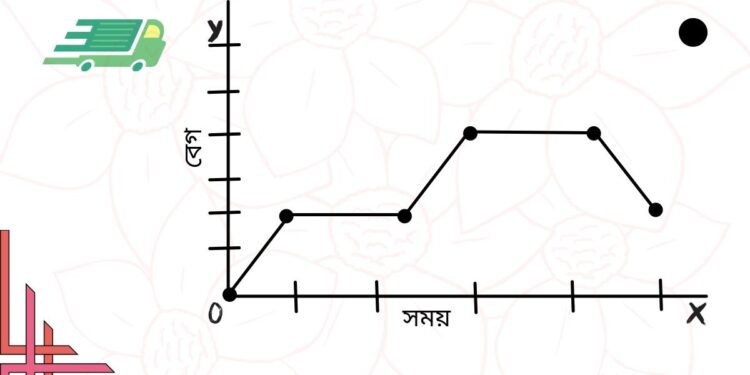
• পাশের লেখচিত্রে একটা বস্তুর সময়ের সাথে বেগের পরিবর্তন দেখানো হয়েছে। এখান থেকে আমরা প্রশ্ন করতে পারি লেখচিত্রে কোথায় ত্বরণ আছে আর কোথায় ত্বরণ নাই?
• আমরা বলতে পারি– A তে ত্বরণ আছে, B তে ত্বরণ নেই, C তে ত্বরণ আছে এবং D তে মন্দন বা নেগেটিভ ত্বরণ আছে।

ত্বরণ ও মন্দন এর প্রকৃতি

উপরের লেখচিত্র থেকে বলতে পারি ত্বরণ ধনাত্মক (কারণ, বেগ বৃদ্ধির হার-ই ত্বরণ) এবং মন্দন ঋণাত্মক (কারণ, বেগ হ্রাসের হার-ই মন্দন)

রৈখিক গতির ক্ষেত্রে – যদি বেগের মানের পরিবর্তন হয় শুধু তাহলেই ত্বরণ হবে। ত্বরণকে ‘a’ দ্বারা প্রকাশ করা হয়।

ত্বরণ এর মাত্রা

ত্বরণ এর একক

ত্বরণ ও মন্দন এর সূত্র

ত্বরণ হচ্ছে বেগের পরিবর্তনের হার। যদি সমত্বরণ হয়, অর্থাৎ সময়ের সাথে সাথে ত্বরণের পরিবর্তন না হয় তাহলে আমরা লিখতে পারি,

এখানে,

• a= ত্বরণ
• v= আদি বেগ
• u= শেষ বেগ
• t= সময়

কাজেই যদি ত্বরণ a জানা থাকেতাহলে কোনো বস্তুর আদিবেগ u হলে t সময় পর তার বেগ v বের করা খুব সহজ।

কোনো বস্তু যদি স্থির অবস্থা থেকে যাত্রা শুরু করে

আমরা পড়ন্ত বস্তুর ক্ষেত্রে লিখতে পারি,

এখানে,

• g= মাধ্যাকর্ষণজনিত ত্বরণ।

যদি কোনো একটা বস্তু স্থির অবস্থা থেকে ছেড়ে দিই তাহলে দেখতে পাই তার গতিবেগ,