শিক্ষা জীবনে গণিত একটি অপরিহার্য বিষয়। এছাড়াও দৈনন্দিন জীবনে বিভিন্ন ক্ষেত্রে এসব গণিতের ব্যবহার হচ্ছে। এর মধ্যে বীজ গণিত অন্যতম। বীজ গণিত শব্দটি ইংরেজি Algebra শব্দের প্রতিশব্দ। এটি আরবি ‘আল জাবের’ থেকে উদ্ভূত হয়েছে।
বীজ গণিত হচ্ছে একটি গাণিতিক পদ্ধতি যা সংখ্যার পরিবর্তে বিভিন্ন বর্ণ বা প্রতিক ব্যবহার করে অজানা রাশির মান বের করে অথবা রাশিসমূহের মধ্যে সম্পর্ক নির্ণয় করে। বীজ গণিতের জনক বা আবিষ্কার বলা হয় আল খোয়ারিজমিকে। নিম্মে বীজ গণিতের গুরুত্বপূর্ণ সূত্রসমূহ দেওয়া হল।
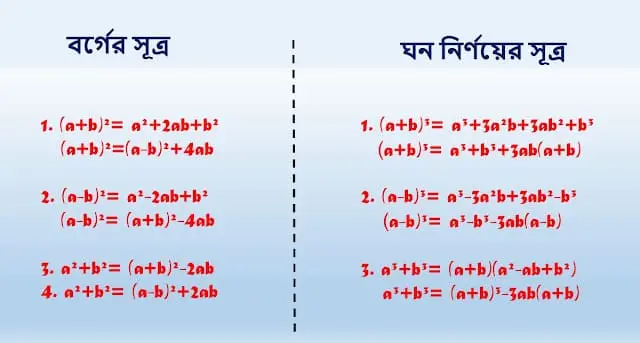
বর্গের সূত্র
1. (a+b)²= a²+2ab+b²
(a+b)²=(a-b)²+4ab
2. (a-b)²= a²-2ab+b²
(a-b)²= (a+b)²-4ab
3. a²+b²= (a+b)²-2ab
4. a²+b²= (a-b)²+2ab
5. a²-b²= (a+b)(a-b)
6. 2(a²+b²)= (a+b)²+(a-b)²
7. a²+b²= ½⟨(a+b)+(a-b)
8. 4ab= (a+b)²-(a-b)²
9. ab= (a+b)²/2 – (a-b)²/2
10. (a+b+c)²= a²+b²+c²+2(ab+bc+ca)
11. a²+b²+c²= (a+b+c)² – 2(ab+bc+ca)
12. 2(ab+bc+ca)= (a+b+c)² – a²+b²+c²
গুণনের সূত্র
13. (x+a)(x+b)= x²+(a+b)x+ab
14. (x+a)(x-b)= x²+(a-b)x-ab
15. (x-a)(x+b)= x²-(a-b)x-ab
16. (x-a)(x-b)= x²-(a+b)x+ab
ঘন নির্ণয়ের সূত্র
1. (a+b)³= a³+3a²b+3ab²+b³ (ঘন নির্ণয়)
(a+b)³= a³+b³+3ab(a+b)
2. (a-b)³= a³-3a²b+3ab²-b³ (ঘন নির্ণয়)
(a-b)³= a³-b³-3ab(a-b)
3. a³+b³= (a+b)(a²-ab+b²) (উৎপাদক নির্ণয়)
a³+b³= (a+b)³-3ab(a+b) (মান নির্ণয়)
4. a³-b³= (a-b)(a²+ab+b²) (উৎপাদক নির্ণয়)
a³-b³= (a-b)³+3ab(a-b) (মান নির্ণয়)