S.F.D and B.M.D অংকন এবং অংকনের নিয়ম এবং ব্যাখ্যা
S.F.D and B.M.D with Rules and Explaination by sbook99
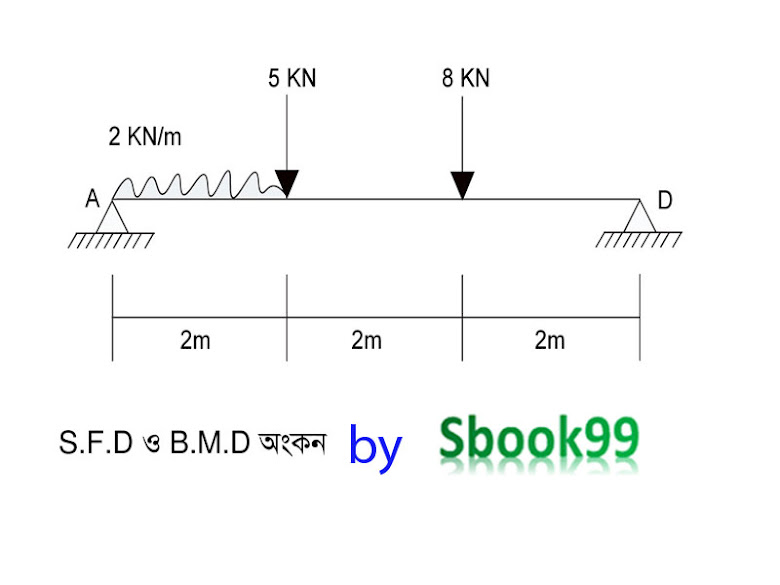
 S.F.D and B.M.D by sbook99
S.F.D and B.M.D by sbook99প্রতিক্রিয়া বল হিসাবঃ
প্রথমে,
A বিন্দুতে মোমেন্ট নেই, ∑ MA = 0 ↓ (+ )
বা, ( 2 × 2 × 1 ) + ( 5 × 2 ) + ( 8 × 4 ) – ( RD × 6) = 0
বা, 4 + 10 + 32 – 6 RD = 0
বা, RD = = 7.67 KN
D বিন্দুতে মোমেন্ট নেই, ∑ MD = 0 ↓ (+ )
বা, ( – 8 × 2 ) + ( – 5 × 4 ) + ( 2 × 2 × 5 ) + ( RA × 6) = 0
বা, – 16 – 20 -20 + 6 RA = 0
বা, RA = = 9.33 KN
সমাধান করার নিয়ম ও ব্যাখ্যাঃ
১. প্রথমে বীমের চিত্রটি দেওয়া আছে সেটা অংকন করে নিতে হবে।
২. এরপর প্রদত্ত লোড এর জন্য প্রতিক্রিয়া বল হিসাব করতে হবে। নিচের মত করে।
যেমন উক্ত চিত্রে, 2 KN/m সমভাবে বিস্তৃত লোড, 5 KN উলম্ব লোড এবং 8 KN উলম্ব লোড রয়েছে। তাহলে A ও D বিন্দুতে প্রতিক্রিয়া বল হিসাব করতে হবে, যেটা আসলে উক্ত দুই বিন্দুতে মোট মোমেন্ট।
মোট মোমেন্ট কে ∑ M দ্বারা প্রকাশ করা হয় এবং ∑ M = 0
ইহা ঘড়ির কাটার দিকে (Clockwise) ধনাত্মক ধরে হিসাব করতে হবে।

[*উপরের চিত্র দুটি শুধুমাত্র বোঝার সুবিধার্থে অংকন করা হয়েছে, অংক করার সময় এটা লাগবে না]
তাহলে A বিন্দুতে মোট মোমেন্ট, ∑ MA = 0 ↓ (+ )
B বিন্দুতে মোট মোমেন্ট, ∑ MD = 0 ↓ (+ )
মোমেন্ট নির্ণয়ের নিয়ম হচ্ছে, মোমেন্ট = বল × লম্ব দুরত্ব
সমভাবে বিস্তৃত বলের বা লোডের ক্ষত্রে,
মোমেন্ট = বল × সমভাবে যতদূর বিস্তৃত তার দুরত্ব × সমভাবে বিস্তৃত লোডের কেন্দ্র হতে মোট দূরত্ব
যেমনঃ উপরের বীমে 2 KN/m এর ক্ষেত্রে, মোমেন্ট = 2 × 2 × 1
কারণ, 2 কে 2 দিয়ে ভাগ করলে সমভাবে বিস্তৃত লোডের কেন্দ্র 1 পাওয়া যায়।
একই ভাবে, 5 KN এর মোমেন্ট = 5 × 2
একই ভাবে, 5 KN এর মোমেন্ট = 8 × 4
একই ভাবে, D এর মোমেন্ট = RD × 6 [R বলতে Reaction বা প্রতিক্রিয়া বুঝায়]
তাহলে, A বিন্দু হতে Clockwise Positive ধরে নিলে A বিন্দুতে মোট মোমেন্ট পাই পাই,
( 2 × 2 × 1 ) + ( 5 × 2 ) + ( 8 × 4 ) – ( RD × 6) = 0
বা, RD = 7.67 KN
একই ভাবে, D বিন্দু হতে Clockwise Positive ধরে নিলে D বিন্দুতে মোট মোমেন্ট পাই পাই,
( – 8 × 2 ) + ( – 5 × 4 ) + ( 2 × 2 × 5 ) + ( RA × 6) = 0
বা, RA = 9.33 KN
৩. এখন Shear Force Diagram অংকন করতে হবে। বাম পাশ হতে শুরু করে কিভাবে লোড সমুহ পুরো বীমের উপর বিন্যস্ত হয়েছে তাই অংকন করতে হবে।
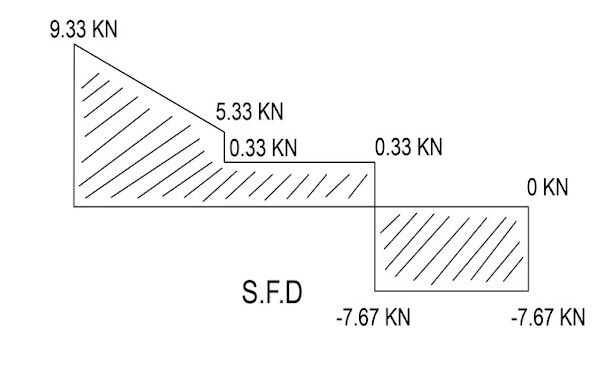
উপরের উদাহরণে A বিন্দুতে মোমেন্ট 9.33 KN, এটা আমরা ধারণা করে একটি লাইন অংকন করে দেই, এরপর 2 KN/m সমভাবে বিস্তৃত লোড = 2 × 2 = 4 KN কে আগের 9.33 KN হতে বিয়োগ করতে হবে, যার মান = 9.33 – 4 = 5.33 KN
9.33 থেকে 5.33 কম এবং সমভাবে বিস্তৃত, তাই 9.33 এর বিন্দু থেকে একটি নিম্নমুখী লাইন পরবর্তী লোড এর দূরত্ব 2 m পর্যন্ত ধারণা করে নেই।
এরপর পরবর্তী লোড কে এর ঠিক আগের লোড হতে বিয়োগ করতে হবে। যেমন এই ক্ষেত্রে 5.33 – 5 = 0.33 KN. এই লোডকে ধারণা করে বীমের দিকে সোজা একটি লাইন অংকন করি এবং যেহেতু এরপরের 8 KN লোড পর্যন্ত কোন লোড নেই, তাই 0.33 KN থেকে 8 KN পর্যন্ত একটি সোজা লাইন অংকন করি।
একইভাবে, 0.33 KN থেকে পরবর্তী লোড 8 KN বিয়োগ করে যা পাই তা ধারণা করা লাইন অংকন করে দেখাতে হবে। যার মান = 0.33 – 8 = – 7.67 KN. যেহেতু ঋণাত্মক মান তাই ইহা বীমের নিচের দিকে চলে যাবে।
এখন, একইভাবে, 7.67 KN হতে পরবর্তী মোমেন্ট 7.67 KN বিয়োগ করে পাই, 7.67 – 7.67 = 0
এই লোড 2 m দুরবর্তী D বিন্দুর সাথে মিলে যাবে।
মিলে না গেলে বুঝতে হবে অংকে কোথাও ভূল হয়েছে।
৪. এরপর Bending Moment Diagram অংকন করতে হবে। পাশাপাশি দুই বিন্দুকে কোন একটি ক্ষেত্র ধরে ইহার ক্ষেত্রফল নির্ণয় করে ইহার মান হিসাব করতে হবে এবং এর সাথে পরের ক্ষেত্রফলের মান যোগ হয়।

যেমন উপরের উদাহরণে, প্রথম দুই বিন্দু একটি ট্রাপিজিয়াম ক্ষেত্র তাই ইহার ক্ষেত্রফল = x (সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য এর যোগফল) x উচ্চতা = 0.5 x (9.33+5.33) x 2 = 14.66 KN-m
ট্রাপিজিয়াম হলে দুই বিন্দুর মাঝে বৃত্ত চাপ এর মত লাইন হয়।
আয়তক্ষেত্র হলে দুই বিন্দুর মাঝে সোজা লাইন হয়।
তারপের দুই বিন্দু একটি আয়তক্ষেত্র, যার ক্ষেত্রফল = দৈর্ঘ্য x প্রস্থ = 0.33 x 2 = 0.66
তাহলে, 14.66 + 0.66 = 15.32 KN-m
এরপর দুই বিন্দুও একটি আয়তক্ষেত্র যার ক্ষেত্রফল = -7.67 x 2 = – 15.34
তাহলে, 15.32 -15.34 = -0.02 = 0 ধরে নেওয়া যায়। অর্থাৎ হিসাব মিলে গেছে।
